Comparing the Arithmetic Mean, Geometry Mean, and Harmonic Mean

The arithmetic mean is what we usually call “average”. You find the arithmetic mean by adding the numbers in a set of data and dividing by the number of pieces of data.

The harmonic mean of a set of numbers is defined as the reciprocal of the arithmetic mean of the reciprocals of the numbers. The harmonic mean for a and b can be computed using

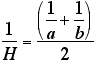
If , then x is called the geometric mean between a and b.

Use a graphing program to investigate and compare these different measures of middle. What can you say about how the arithmetic mean compares to the geometric mean and the harmonic mean?