Inscribed Circle
Draw a circle with radius = 2 units. Draw a square (BEST) around the circle so that each side of the square touches the circle. Draw perpendicular diameters so that the circle and the square are each cut into four equal parts. The circle is cut into four equal sectors while the square is cut into four equal squares.
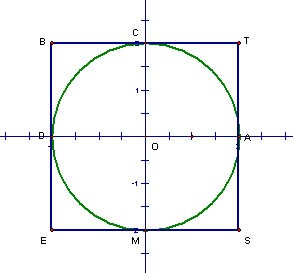
What is the area of square BEST? Of square COAT?
Let’s call the radius of the circle r. In terms of r, what is the area of square BEST? Of square COAT? Of square BDOC? Of rectangle CTSM? Of the concave hexagon CODEST?
Is the area of the circle smaller or larger than the area of square BEST? Why? Is the area of the circle smaller or larger than the area of concave hexagon CODEST? Why?
How can you use this situation to show that the area of a circle equals approximately 3r2?
(Source: Adapted with permission from Addenda Series for Measurement in the Middle Grades, copyright 1994 by the National Council of Teachers of Mathematics. All rights reserved.)
