Tangential Circles
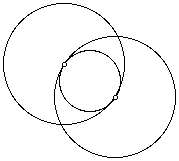
Two larger circles with equal radii pass through each other’s centers. A smaller circle can be created inside the overlapping region so that it is tangent to the other circles. (Tangent means that the circles touch each other but do not cross over each other, nor do they leave any gaps.) Compare the area and circumference of the smaller circle to the area and circumference of the larger circle.
Explain why the rule works.
![]() Extension:
Extension:
How do the results change if the two larger circles do not have equal radii?
