Unit Fractions and Fibonacci
Let s[j], j=0,1,2,… be a sequence of integers that satisfy the recurrence relation s[k] = s[k-1] + s[k-2] with arbitrary initial values s[0] and s[1] (Note that if s[0] = 1 and s[1] = 1, then it is the Fibonacci Sequence). Use spreadsheet software to observe that for any integers m, n with m>n we have
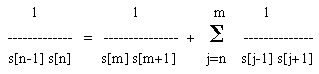
For example, setting s[0]=s[1]=1 and n=5, m=10 gives
1/(s[4].s[5]) = 1/(s[10].s[11]) + 1/(s[4].s[6]) +1/(s[5].s[7]) +1/(s[6].s[8]) +1/(s[7].s[9]) +1/(s[8].s[10]) +1/(s[9].s[11])
In other words,
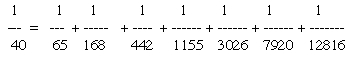
Click here for a spreadsheet.
How can we use this observation to represent any given unit fraction as sum of certain number of unit fractions (e.g. 1/a as sum of b unit fraction)?
![]() Extension:
Extension:
How can we use above relation to generate integer solutions of the harmonic equation
