Squaring with Squares
One of the proofs of the Pythagorean Theorem typically uses squares constructed on each side of a right triangle (see figure below). The area of the square constructed on the hypotenuse (green square) is equal to the sum of the areas of the squares constructed on each of the legs of the triangle (blue squares).
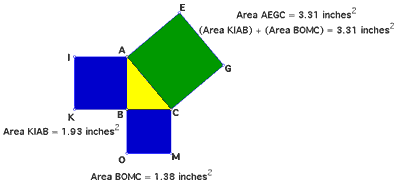
Instead of using squares, can we use equilateral triangles? How about regular hexagons? Would these figures (or any others) give the same results?
What is so special about squares? In other words, why are squares typically used in this proof?
View a dynamic version of this construction in GSP
