Divide into n-th Segment

Take a equilateral triangle, divide each side into 4 segments. Then connect the each vertex to division points on the opposite sides as you observe in the Figure 1.

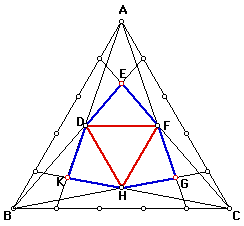
What can be said about the hexagon DEFGHK formed by the intersections points of the respective segments? Is it regular?
What can be said about the triangle DFH? What kind of a triangle is this? What is the relation between area of ABC and area of DFH?

Extension 1
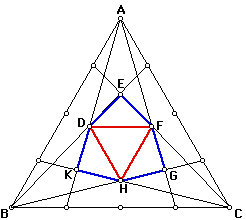
Take a equilateral triangle, divide each side into 5 segments. Then connect the each vertex to division points on the opposite sides as you observe in the Figure 2. And answer the above questions for this case.

Extension 2:
Can you make general statements about the answers of the above questions in the case that each side of the equilateral triangle is divided into n segment?

Extension 3:
Now take a square and divide each side into n equal segment. Connect the each vertex to the first n-th segment on the opposite two sides. Figure 3 shows the case for n=5.

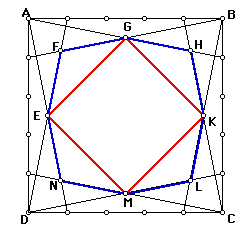
What can be said about the octagon EFGHKLMN (blue one)? Is it regular? Etc…
What can be said about the quadrilateral EGKM (red one)? Is it a square? What is the relation between area of ABCD and EGKM? Can you make a generalization for the general case (i.e. EGKM formed after dividing each side into n equal segment)?

Extension 4:
Take any regular polygon and divide each side into n equal segment. Try to form regular shapes and observe their properties by connecting certain intersection points as we did in equilateral triangle and square case above.