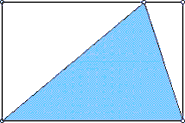
A triangle has two shared vertices and one shared side with a rectangle. The third vertex is anywhere on the side opposite of the shared side (see figures above).
How does the area of the triangle compare with the area of the rectangle? Why do you think this relationship holds?
Extension:
Where would you move the third vertex of the triangle to have a minimum perimeter? Explain why this position results in a minimum perimeter.
